Introduction
We have all played puffcap decks at some point, and we have all become frustrated after our opponent drew zero traps even if their deck was full of them.
After losing many matches with this archetype, I gathered a few players who are also math teachers and engineers to help me understand the math behind puffcaps in Runeterra.
They set me up with a calculator to help me understand the chances of my enemy drawing X puffcaps depending on the number of cards in their deck, and puffcaps shuffled.
Understanding How Puffcaps Work

To understand how the calculator works, first we need to understand how puffcaps work.

When you shuffle puffcaps into your opponent's deck, you're adding an effect to a random card in your opponent's deck. This effect is: deal 1 damage to the Nexus when you draw me. So, when your opponent draws this card with puffcaps, it activates its effect: "When you draw me, deal 1 damage to your Nexus."
Runeterra decks have 40 cards. On turn 1, you start the game with 4 cards in your hand + the first card you draw. This means each player has 5 cards in their initial hand on turn 1, which means they'll have 35 cards in their deck at that moment. If in any way your opponent has 1 puffcap in their deck, their chances of drawing it on turn 1 will always be (1/35), or 2.85% chance. The numbers start to get complicated when you shuffle more and more puffcaps.
To know exactly what are the odds of drawing an X number of puffcaps, you also need to consider the chances of them not drawing these puffcaps.
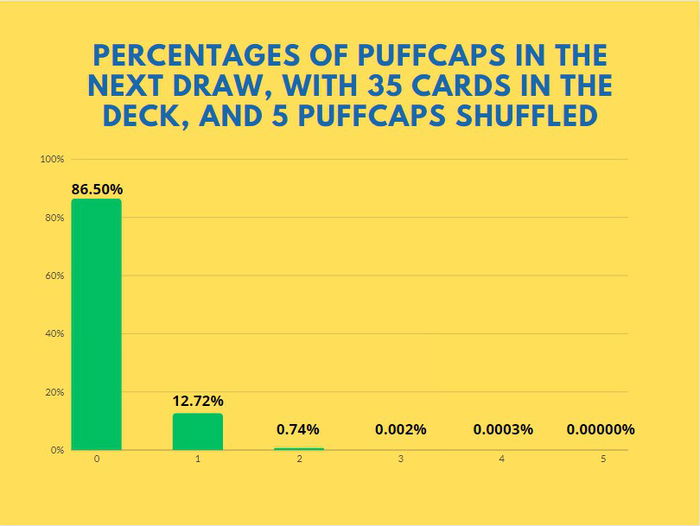
If you shuffle 5 puffcaps into your opponent's deck right away on turn 1, the chances of them drawing 1 puffcap on the next turn is translated into the formula: 5(1/35^1(34/35)^4 or 12.72%).
It is easier to visualize this formula in graphs because this way we can get a better notion of the numbers while we compare them to other results that we might like to know about. The following graph shows exactly the total of the formula I've written above, compared to the results of the chance % of your opponent drawing other amounts of puffcaps.
Analyzing the Odds of Common Cases
Now that you already know how we calculate the chance % of drawing puffcaps, let's play with these numbers a bit and put into practice some common cases.
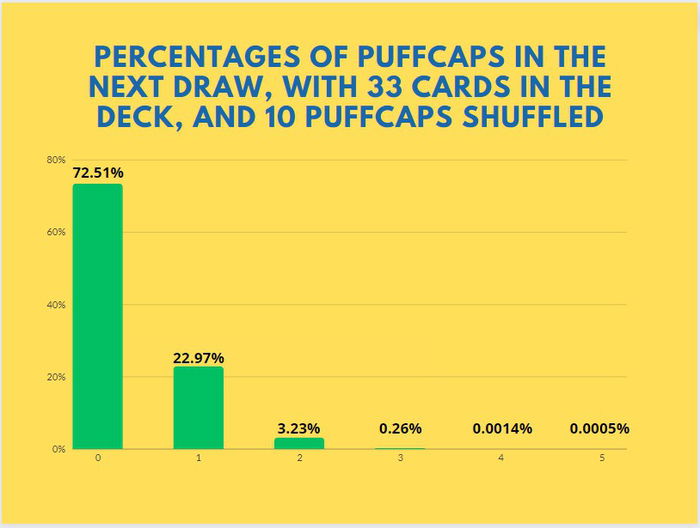
For instance: Let's assume your opponent has attacked twice with their Teemo and you want to know what are the odds of them taking damage through puffcaps on the next turn. The graph below shows the percentages in case your opponent is attacking on odds and managed to summon and attack with Teemo already on turn 1. Notice that we're calculating percentages with 33 cards in the deck because this is the number of cards your deck would have in a usual match after your opponent attacked twice with their Teemo. Considering Teemo attacked twice, we're also calculating 10 puffcaps shuffled into their deck.
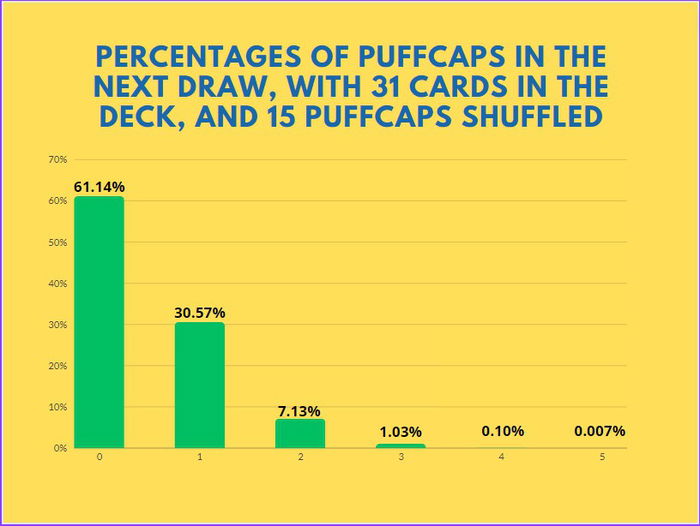
Now let's see how this graph turns out if Teemo attacks a third time.
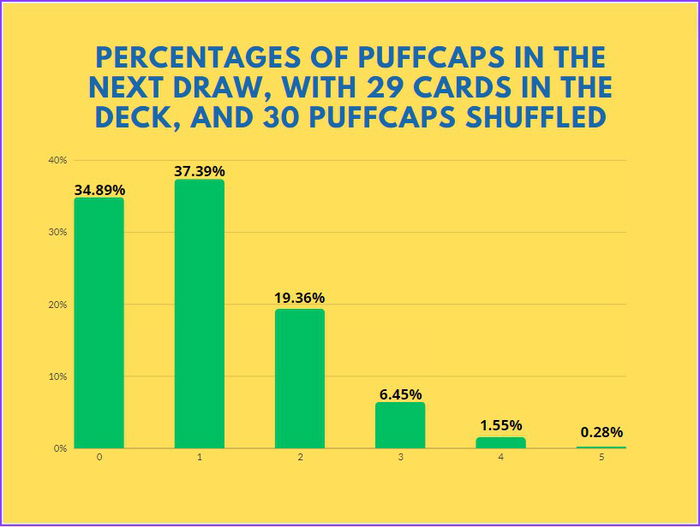
The next graph shows percentages after a fourth Teemo attack, with him at level 2 doubling puffcaps.
And, just as a curiosity, this is how the graph is after level 2 Teemo hits the Nexus a second time.
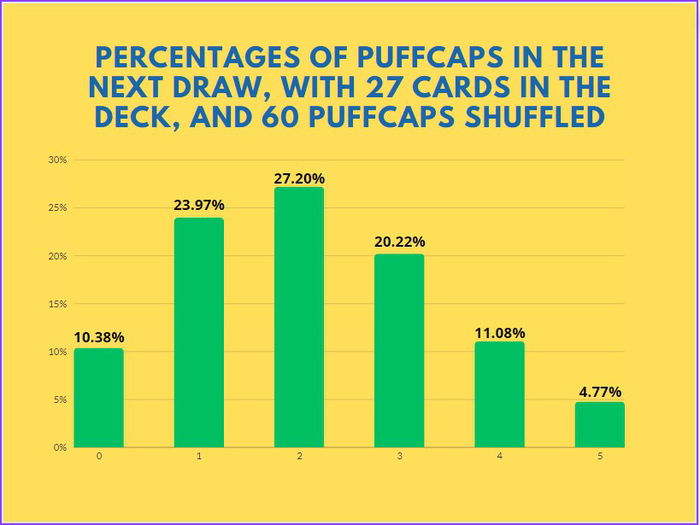
Obviously, these results are a bit unrealistic because, as the graphs themselves indicate, the chances of drawing a puffcap, according to how many times Teemo attacks, are huge. So, consider that, to have an exact result, you need to calculate, instead of 60 puffcaps shuffled, 57 or 56, because you'll probably draw 3 or 4 puffcaps until Teemo hits a second time at level 2. Don't worry, though, because I created this more realistic graph for you:
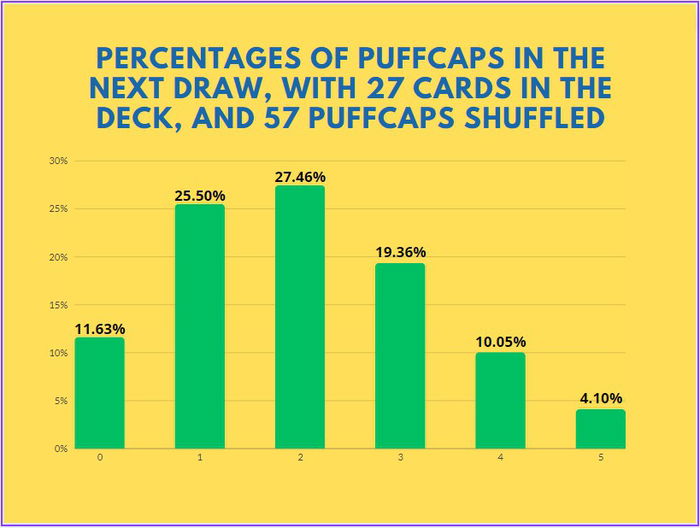
Now, let's analyze a common case, but an extremely specific one. You've played a Chump Whump on turn 4, and on turn 5 you play a Puffcap Peddler. You still have 2 usual mana and 3 spell mana. You play two Mushroom Clouds, and protect your Puffcap Peddler with a Sky Splitter. In all, 19 puffcaps were shuffled into your opponent's deck, and you're on turn 5, so they have 31 cards in their deck.
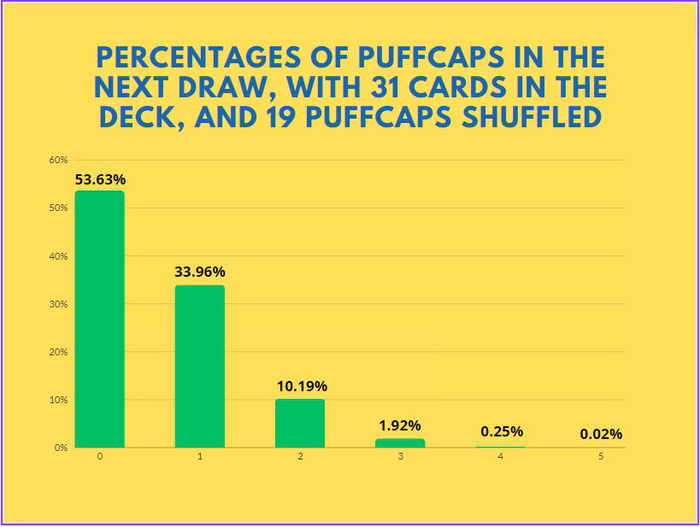
We can analyze, with these graphs, that puffcaps are only efficient long term, or if you can shuffle an absurd number of puffcaps in your opponent's deck. With 60 puffcaps and 27 cards, your opponent will probably draw just 2 puffcaps, which is a very disproportionate number when compared to 60. Considering that, to shuffle 60 puffcaps, you most likely had to attack 4 times with Teemo, and avoid several removals, it is clear that this mana investment is quite absurd for your result to be the great odds of drawing just 2 puffcaps.
Analyzing the Odds in Absurd Cases
Let's see a few absurd cases to have a better notion of how bad it is to invest your mana in puffcaps.
In the next graph, we shuffled 100 puffcaps into 25 cards.
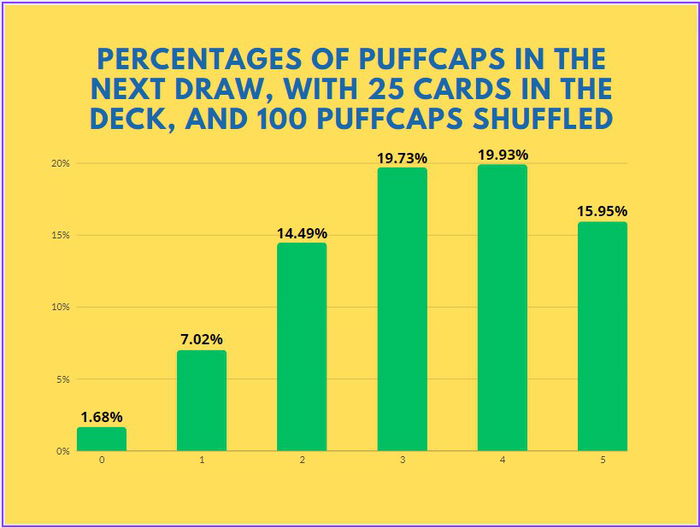
To deal 3 damage to the enemy Nexus, you can play a Noxian Fervor, or attack with a Legion Saboteur on turn 1, or play a Blowback, instead of shuffling 100 puffcaps.
Now, we shuffled 150 puffcaps into 20 cards.
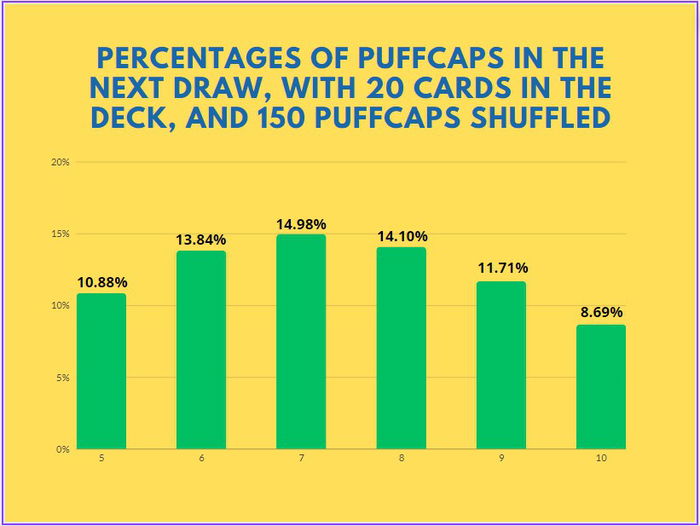
Notice that, as we add more puffcaps and fewer cards, the percentages get more balanced. In the graph above, we have the odds of drawing 5 to 10 puffcaps, all around 12%.
Now, let's assume you obliterated your opponent's deck with Maokai, and shuffled 150 puffcaps next.
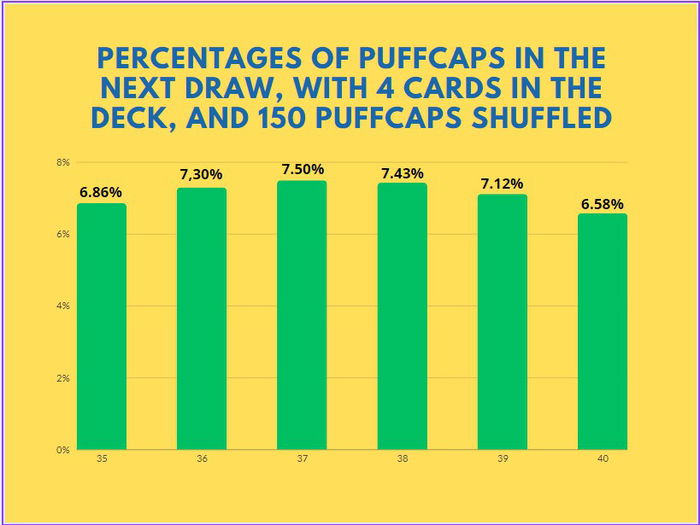
The chances of them drawing 35 to 40 puffcaps are very similar in this situation.
After All, are Puffcaps a Strong Mechanic?

Puffcaps are not a strong mechanic on their own. A puffcap deck focused on winning matches through their direct damage isn't consistent at all. Puffcaps are only strong when your opponent draws an elevated number of cards per turn, like Sunken Temple lists, or when your opponent works with a very reduced number of cards, like Deep lists.
Apart from these cases, it is very difficult to deal more than 3 damage to the enemy Nexus during a match using puffcaps in a meta deck that brings Teemo, that isn't entirely focused, 100%, on the puffcap mechanic itself. They are just a bonus that you create during a match that can help you, even if just a little, win games.
Invest your mana on puffcaps wisely!
Final Words

I would like to thank my friends in the Brazilian community, "Falquetto" for teaching me how to do the math for this article, and "Insulinado" for creating for me the puffcap calculator! I'll leave a link for the calculator below if you want to play with it as well - here.
Don't forget to share this article on social media. See you next time!













— Comentarios 0
, Reacciones 1
Se el primero en comentar